선형 자료 구조란 요소가 일렬로 나열되어 있는 자료 구조를 뜻한다.
연결 리스트
연결 리스트는 데이터를 감싼 노드를 포인터로 연결해서 공간적인 효율성을 극대화 시킨 자료구조
삽입/삭제: O(1)
탐색: O(n)

위의 그림처럼 prev 포인터와 next 포인터로 앞과 뒤의 노드를 연결시킨 것이 연결 리스트이다.
- 싱글 연결 리스트: next 포인터만 가짐.
- 이중 연결 리스트: next 포인터와 prev 포인터를 가짐.
- 원형 이중 연결 리스트: 이중 연결 리스트와 같고, 마지막 노드의 next 포인터가 head 노드를 가리킴.
#include<iostream>
#include<list>
using namespace std;
int main() {
list<int> a;
a.push_front(0);
a.push_back(1);
a.push_back(2);
auto it = a.begin(); it++;
a.insert(it, 1000);
a.pop_front();
a.pop_back();
cout << a.front() << endl; // 출력: 1000
cout << a.back() << endl; // 출력: 1
}
배열
배열은 같은 타입의 변수들로 이루어진, 크기가 정해져 있고, 인접한 메모리 위치에 있는 데이터들의 집합
*여기서 말하는 배열은 정적 배열을 기준으로 합니다.
삽입/삭제: O(n)
접근(참조): O(1) - 랜덤접근 가능
랜덤 접근과 순차적 접근
랜덤 접근(직접 접근)은 배열과 같은 순차적인 데이터가 있을 때 임의의 인덱스에 해당하는 데이터에 접근.
데이터를 특정 위치에 바로 접근할 수 있는 방식입니다. 모든 데이터는 위치에 상관없이 동일한 시간 안에 접근 가능.
순차 접근은 데이터를 저장된 순서대로 접근하는 기능. 데이터를 처음부터 차례대로 순서대로 접근한다.
배열과 연결 리스트 비교
배열은 상자를 순서대로 나열한 데이터 구조이고, 몇번째 상자인지만 알면 해당 상자의 내용물을 알 수 있음.
연결 리스트는 상자를 선으로 연결한 데이터 구조이고, 상자의 내용물을 알기 위해서는 상자 하나하나씩 내부를 확인해 봐야 한다.
배열은 삽입, 삭제 시 모든 상자의 내용물을 이동시켜야 하지만, 연결 리스트는 선을 바꿔서 연결만 하면 된다.
=> 데이터 추가, 삭제가 많으면 연결 리스트, 접근(참조)이 많으면 배열이 좋음
벡터
벡터는 동적으로 요소를 할당할 수 있는 동적 배열
맨 뒤의 삽입/삭제: O(1) - push_back()
그 외의 삽입/삭제: O(n)
접근: O(1) - 랜덤접근 가능
push_back()을 하면 2의 제곱승 + 1 마다 크기를 2배로 늘림
| 함수 | 용량 | 비용 | |
| push_back(1) | 1 | 1 | 1 |
| push_back(2) | 2 | 1 + 1 | 1 2 |
| push_back(3) | 4 | 2 + 1 | 1 2 3 _ |
| push_back(4) | 4 | 1 | 1 2 3 4 |
| push_back(5) | 8 | 4 + 1 | 1 2 3 4 5 _ _ _ |
| push_back(6) | 8 | 1 | 1 2 3 4 5 6 _ _ |
| push_back(7) | 8 | 1 | 1 2 3 4 5 6 7 _ |
| push_back(8) | 8 | 1 | 1 2 3 4 5 6 7 8 |
Ci 를 i 번째 push_back()을 했을 때 드는 비용이라고 하면, Ci 는 1 또는 1 + 2^k 이고,
-> n번 push_back()을 했을 때 드는 비용 T(n)은 아래와 같다.

이를 n으로 나눠 평균적으로 드는 비용을 계산하면 3이기에, 상수 시간에 가까운 amortized(암묵적 상수 시간)복잡도를 가진다.
따라서 push_back()은 O(1)의 시간 복잡도를 가진다.
#include <iostream>
#include <vector>
#include <algorithm> // find 함수
using namespace std;
int main() {
vector<int> v;
v.push_back(1); v.push_back(2); v.push_back(3);
v.pop_back();
v.erase(v.begin(), v.begin() + 2); // 0~1 인덱스를 삭제
auto a = find(v.begin(), v.end(), 3);
v.clear();
}스택
LIFO (Last In First Out)를 따르는 자료구조
재귀함수, 알고리즘에 사용됨. 웹 브라우저 방문 기록에 사용됨.
삽입/삭제: O(1)
탐색: O(n)

#include <stack>
#include <iostream>
using namespace std;
int main(){
stack<int> stk;
stk.push(1);
stk.pop();
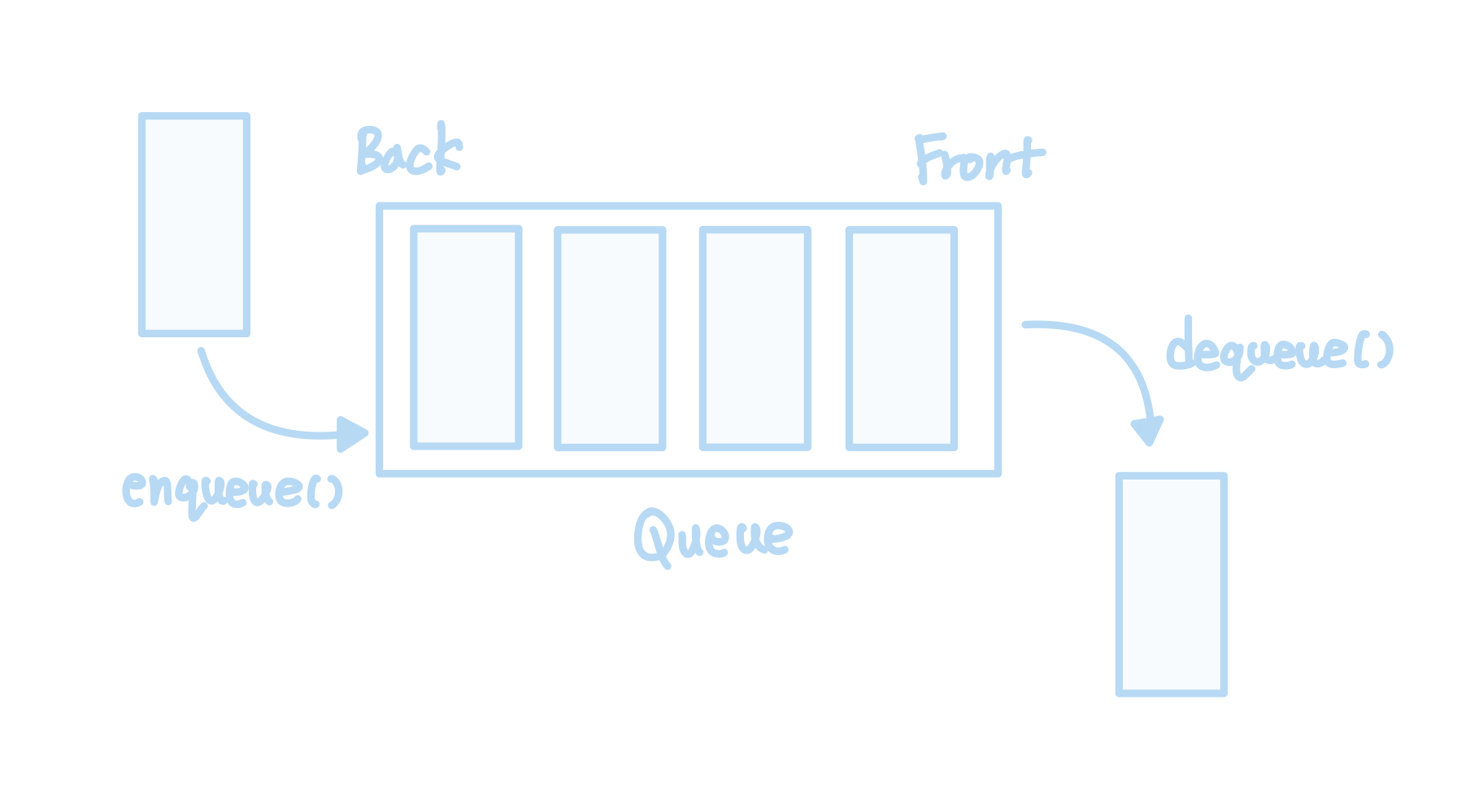
}큐(Queue)
FIFO (First In First Out)를 따르는 자료구조
CPU 작업을 기다리는 프로세스, 스레드 행렬 또는 네트워크 접속을 기다리는 행렬, 너비 우선 탐색, 캐시 등에 사용됨.
양쪽 끝에서 연산이 이루어진다.
- 삽입은 큐의 뒤쪽(rear/back)에서 이루어지며,
- 삭제는 큐의 앞쪽(front)에서 이루어집니다.
삽입/삭제: O(1)
탐색: O(n)
#include <iostream>
#include <queue>
using namespace std;
int main() {
queue<int> q;
// enqueue
q.push(10);
q.push(20);
q.push(30);
// front element
cout << "Front: " << q.front() << endl; // 10
// dequeue
q.pop(); // 10 제거
// front element
cout << "Front after dequeue: " << q.front() << endl; // 20
}덱(Deque)
양쪽 끝에서 데이터의 삽입과 제거가 가능한 자료구조
Deque는 Double-Ended Queue의 줄임말. 큐와 스택의 기능을 모두 가지고 있어 매우 유연하게 사용 가능.
삽입/삭제: O(1)
탐색: O(n)
양쪽 끝에서 삽입과 삭제
- 앞(front)과 뒤(back) 모두에서 데이터를 삽입하고 제거할 수 있습니다.
- 이를 통해 덱은 스택(LIFO, Last-In-First-Out)처럼 사용할 수도 있고, 큐(FIFO, First-In-First-Out)처럼 사용할 수도 있습니다.
덱은 일반적으로 동적 배열 또는 이중 연결 리스트로 구현됨.
- 동적 배열 기반: 배열의 양쪽 끝에서 삽입과 삭제를 지원하기 위해 원형 구조로 구현 가능.
- 장점: 배열을 사용하기 때문에 인덱스를 통해 빠르게 데이터에 접근할 수 있습니다.
- 단점: 배열의 크기가 고정되면 크기를 재조정하는 작업이 필요할 수 있습니다.
- 이중 연결 리스트 기반: 덱을 이중 연결 리스트로 구현하면 양쪽 끝에서의 삽입과 삭제가 효율적임.
- 장점: 크기가 동적이므로 데이터가 추가될 때마다 리스트가 자동으로 확장됩니다.
- 단점: 중간 데이터에 대한 접근이 배열보다 느립니다.
#include <iostream>
#include <deque>
using namespace std;
int main() {
deque<int> dq;
// push_front, push_back
dq.push_back(10); // [10]
dq.push_front(20); // [20, 10]
dq.push_back(30); // [20, 10, 30]
// pop_front, pop_back
dq.pop_front(); // [10, 30]
dq.pop_back(); // [10]
// front, back
cout << "Front: " << dq.front() << endl; // 10
cout << "Back: " << dq.back() << endl; // 10
}
'CS 스터디' 카테고리의 다른 글
| [자료 구조] - 복잡도 (1) | 2024.10.16 |
|---|---|
| [네트워크] HTTP/1.0/1.1/2/3 (1) | 2024.10.12 |
| [네트워크] - IP 주소 (0) | 2024.10.10 |
| [네트워크] 네트워크의 기초 - 처리량, 지연시간, 네트워크 토폴로지 (2) | 2024.10.06 |